Go back to RESOURCES
Vessel Flow Characterization
The endothelial response to flow-induced stress (e.g., the generation and secretion of nitric oxide) is an important modulator of vascular tone and function, linking vasodilation and constriction to the dynamics of fluid flow. IonWizard’s FloAcq acquisition module is the first to perform real-time calculations of important indicators of arterial flow, including shear stress. The following lists some FloAcq outputs and how they could be applied to the characterization of vascular physiology and function:
MEAN PRESSURE
The mean pressure is simply an average of the input and output pressures. It is useful to monitor when inducing flow. Mean pressure should be constant to ensure that vasodilation is flow-mediated rather than pressure-mediated
VASCULAR RESISTANCE
The vascular resistance is a definition of the force opposing the movement of solution through a vessel. It is inversely related to vessel diameter. A greater vascular resistance will require a greater degree of vasodilation in order to maintain constant pressure within the vessel.
SHEAR STRESS
Shear stress is a characterization of the frictional drag exerted on arterial walls during flow. Shear stress is of particular importance to vascular function. It has been linked to the release of vasoactive substances as well as the regulation of gene expression, cellular metabolism, and morphology. In contrast to stretching, which acts as a circumferential force in response to pressure, shear stress is a tangential force applied along the endothelium. Normal levels of shear stress serve to maintain wall physiology and vascular homeostasis. High shear stress triggers vasodilation in order to regulate the mechanical forces exerted on arterial walls, often referred to as “endothelium-dependent flow-mediated dilatation”.
REYNOLDS NUMBER
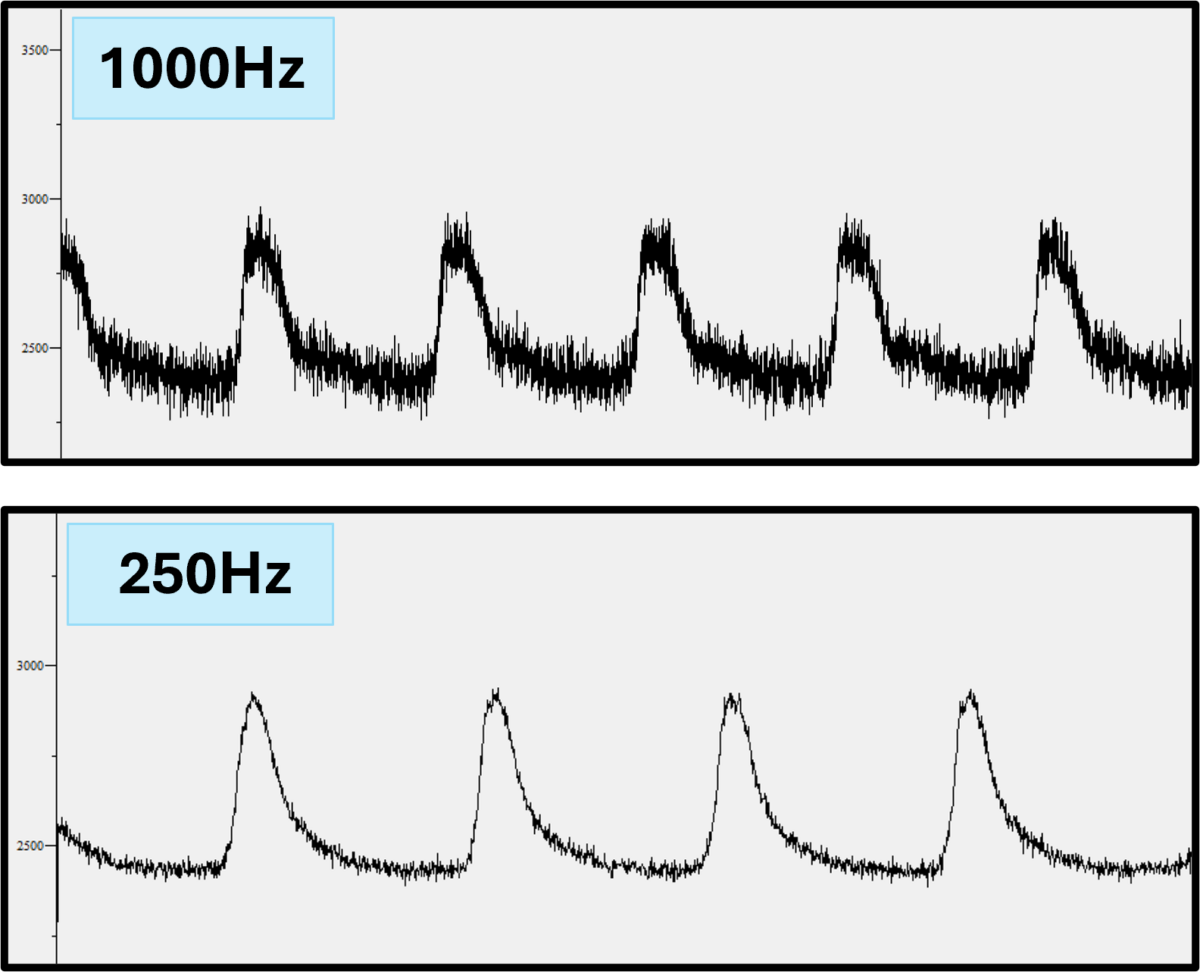
The Reynolds number, Re, describes whether the flow is either turbulent or laminar. A very large Re (≥2000) suggests turbulent flow, where nonaxial flow instabilities increase stress on blood vessels. Turbulence-induced shear stress triggers nitric oxide synthesis in the endothelium which leads to relaxation of smooth muscle cells and restoration of laminar flow in normal healthy tissue. High Re values occur from high flow volume in narrow vessels, high flow velocity, branching (bifurcations), etc. Laminar flow exists at lower Re, although laminar vortices may be driven by inertial forces. At much lower Re, where flow is dominated by very viscous forces, inertial force becomes negligible and flow stops.
FORMULAS
These calculations are based on raw inputs (typically generated by a flow meter and pressure interface accompanying a myography system) and vessel diameter outputs (such as our VesAcq dimensioning software). The following lists the formulas used both in VesAcq and FloAcq to calculate real-time values:
Mean Pressure = (Pin+Pout)/2; where Pin is the input pressure and Pout is the output pressure.
Vascular Resistance = Pdiff/Q; where Pdiff is the pressure difference and Q is the volume flow.
Shear Stress = (8*η*V)/Di; where η (eta) (sometimes represented as µ, or mu) is the dynamic viscosity, V is the flow velocity and Di is the inner diameter of the vessel.
Reynolds Number = ρ*V*Di/η; where ρ (rho) is the density, V is the flow velocity, Di is the inner diameter, and η (eta) is the dynamic viscosity.
FOR FURTHER READING
The following citations are predominately review articles that give either an explanation of fluid dynamics as they relate to vascular biology or focus on endothelial mechanotransduction, or both:
- GM Buga, ME Gold, JM Fukuto and LJ Ignarro. Shear stress-induced release of nitric oxide from endothelial cells grown on beads. Hypertension (1991) 17:187-193.
- Shu Chien. Mechanotransduction and endothelial cell homeostasis: the wisdom of the cell. Am J Physiol Heart Circ Physiol (2007) 292: H1209-H1224.
- Kristopher S Cunningham and Avrum I Gotlieb. The role of shear stress in the pathogenesis of atherosclerosis. Laboratory Investigation (2005) 85: 9–23. (Please note that the units given for Re in this reference are incorrect. Re is a ratio of forces, inertial over viscous; the result of which should be dimensionless.)
- Peter F. Davies. Flow-mediated endothelial mechanotransduction. Physiological Reviews (1995) 75:519-560. Groenendijk, et al. The role of shear stress on ET-1, KLF2, and NOS-3 expression in the developing cardiovascular system of chicken embryos in a venous ligation model. Physiology (2007) 22: 380-38. Kyra E Pyke and Michael E Tschakovsky. The relationship between shear stress and flow-mediated dilatation: implications for the assessment of endothelial function.
- The Journal of Physiology (2005) 568: 357-369. Oren Traub and Bradford C. Berk. Mechanisms by Which Endothelial Cells Transduce an Atheroprotective Force. Arteriosclerosis, Thrombosis, and Vascular Biology (1998) 18:677-685.
APPENDIX: VesAcq Values
In addition to outer and luminal diameters, VesAcq performs the following measurements and calculations in real time:
WALL THICKNESS
Wall thickness is often used to determine if the preparation is hypertrophied; the thicker the wall, the greater the degree of hypertrophy.
Wall Thickness = (De-Di)/2; where De is the outer or external diameter of the vessel and Di is the luminal or inner diameter
CROSS SECTIONAL AREA
Similar to wall thickness, cross sectional area is useful as an indication and measure of hypertrophy.
Cross Sectional Area = (π/4)*[(De)2 – (Di)2]; where De is the outer or external diameter of the vessel and Di is the luminal or inner diameter.
MEDIA/LUMEN RATIO
The media/lumen ratio is indicative of morphological changes and can be used along with wall thickness and cross sectional area to determine the particular form of hypertrophy.
Media/Lumen Ratio = (De – Di)/(Di); where De is the outer or external diameter of the vessel and Di is the luminal or inner diameter.
Please download the following pdf for a digital copy of this page.